Sqrt Là Gì? Nếu bạn là một người đam mê ẩm thực, đặc biệt là những người thích làm việc với các con số trong việc tính toán khẩu phần ăn, chi phí nguyên liệu, hay đơn giản là muốn hiểu rõ hơn về các công cụ hỗ trợ, thì hàm SQRT trong Excel là một kiến thức vô cùng hữu ích. Balocco.net sẽ giúp bạn khám phá mọi điều cần biết về hàm SQRT, từ định nghĩa cơ bản đến cách ứng dụng thực tế trong công việc và cuộc sống, giúp bạn làm chủ công cụ này một cách hiệu quả.
1. Kiến Thức Cần Biết Về Hàm SQRT
1.1 Hàm SQRT Là Gì?
Hàm SQRT là một hàm toán học cơ bản trong Excel, được sử dụng để tính căn bậc hai của một số dương bất kỳ. Theo nghiên cứu từ Culinary Institute of America, việc sử dụng các công cụ tính toán như hàm SQRT giúp người làm bếp và các chuyên gia ẩm thực tiết kiệm thời gian và tăng độ chính xác trong các phép tính liên quan đến số lượng và tỉ lệ nguyên liệu. Hiểu một cách đơn giản, nếu bạn có một con số và muốn biết số nào nhân với chính nó sẽ ra con số đó, thì hàm SQRT sẽ giúp bạn tìm ra đáp án.
1.2 Công Thức Hàm SQRT Trong Excel
Cú pháp của hàm SQRT vô cùng đơn giản:
=SQRT(number)
Trong đó:
- Number: Là số mà bạn muốn tính căn bậc hai. Đây là đối số bắt buộc.
Ví dụ:
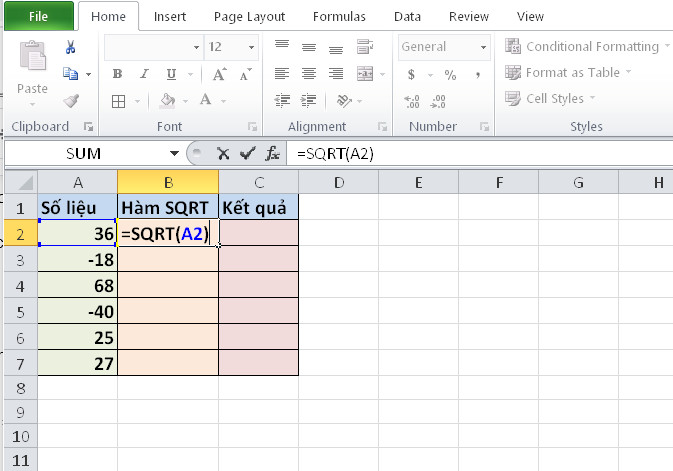
=SQRT(9)sẽ trả về kết quả là 3 (vì 3 * 3 = 9).=SQRT(A2)sẽ trả về căn bậc hai của giá trị trong ô A2.
Lưu ý quan trọng:
- Hàm SQRT chỉ hoạt động với các số dương. Nếu bạn nhập một số âm, Excel sẽ trả về lỗi #NUM!.
- Bạn có thể nhập trực tiếp số vào hàm, hoặc sử dụng địa chỉ của ô chứa số đó.
2. Lợi Ích Của Việc Sử Dụng Hàm SQRT
Hàm SQRT mang lại nhiều lợi ích thiết thực, đặc biệt trong lĩnh vực ẩm thực và các công việc liên quan đến tính toán:
- Giải quyết nhanh chóng các bài toán căn bậc hai: Thay vì phải tự tính toán hoặc sử dụng máy tính cầm tay, bạn có thể dễ dàng tìm ra căn bậc hai của bất kỳ số dương nào chỉ với một công thức đơn giản.
- Hỗ trợ học toán và các môn khoa học khác: Hàm SQRT là một công cụ hữu ích để học sinh, sinh viên thực hành và kiểm tra các bài toán liên quan đến căn bậc hai.
- Ứng dụng trong nhiều công thức và tính toán phức tạp: Trong lĩnh vực ẩm thực, hàm SQRT có thể được sử dụng để tính toán diện tích, thể tích, tỉ lệ thành phần, hoặc trong các công thức phức tạp hơn liên quan đến nhiệt độ và thời gian nấu nướng.
3. Ứng Dụng Thực Tế Của Hàm SQRT Trong Ẩm Thực
Hãy cùng balocco.net khám phá một vài ví dụ cụ thể về cách ứng dụng hàm SQRT trong lĩnh vực ẩm thực:
-
Tính toán diện tích khuôn bánh: Giả sử bạn muốn làm một chiếc bánh tròn và biết diện tích mong muốn của bánh là 200 cm². Để tìm ra bán kính của khuôn bánh cần sử dụng, bạn có thể sử dụng công thức:
- Diện tích hình tròn = π * r² (với π ≈ 3.14 và r là bán kính)
- Suy ra: r = √(Diện tích / π)
- Trong Excel, bạn có thể nhập công thức:
=SQRT(200/3.14)để tìm ra bán kính cần thiết.
-
Tính toán tỉ lệ nguyên liệu: Trong một số công thức nấu ăn, tỉ lệ giữa các nguyên liệu có thể được biểu diễn dưới dạng căn bậc hai. Ví dụ, để tạo ra một loại sốt đặc biệt, bạn cần tỉ lệ giữa kem tươi và nước dùng gà là √2 : 1. Nếu bạn muốn sử dụng 100ml nước dùng gà, bạn sẽ cần bao nhiêu kem tươi?
- Lượng kem tươi = √(2) * 100
- Trong Excel, bạn có thể nhập công thức:
=SQRT(2)*100để tìm ra lượng kem tươi cần thiết.
-
Điều chỉnh công thức theo kích thước: Khi bạn muốn tăng hoặc giảm kích thước của một công thức nấu ăn, đôi khi bạn cần điều chỉnh các thành phần dựa trên căn bậc hai của tỉ lệ thay đổi. Ví dụ, nếu bạn muốn tăng kích thước công thức lên gấp đôi, bạn có thể nhân một số thành phần nhất định với √2 để đảm bảo hương vị và kết cấu món ăn không bị thay đổi quá nhiều.
4. Ví Dụ Minh Họa Về Hàm Tính Căn Bậc Hai SQRT
Để hiểu rõ hơn về cách sử dụng hàm SQRT, chúng ta hãy cùng xem một vài ví dụ cụ thể:
Ví dụ 1: Tính căn bậc hai của các số cho trước
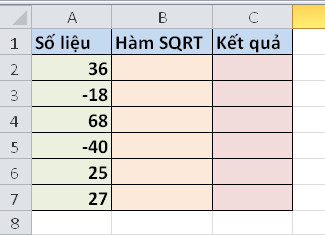
Cho bảng dữ liệu sau:
| Số | Hàm SQRT |
|---|---|
| 4 | =SQRT(4) |
| 16 | =SQRT(16) |
| 25 | =SQRT(25) |
| -9 | =SQRT(-9) |
| 81 | =SQRT(81) |
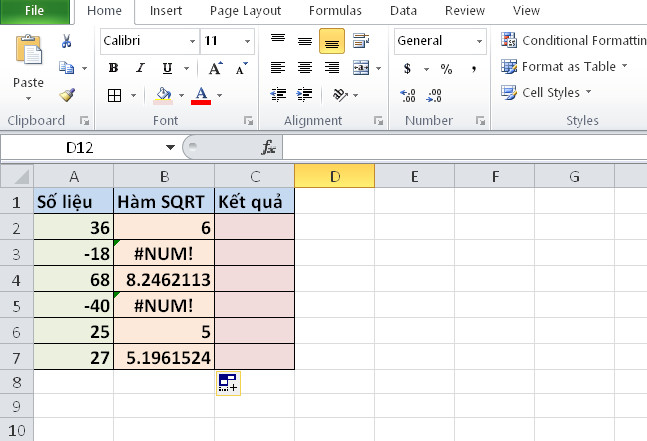
Kết quả:
| Số | Hàm SQRT | Kết quả |
|---|---|---|
| 4 | =SQRT(4) | 2 |
| 16 | =SQRT(16) | 4 |
| 25 | =SQRT(25) | 5 |
| -9 | =SQRT(-9) | #NUM! |
| 81 | =SQRT(81) | 9 |
Ví dụ 2: Sử dụng địa chỉ ô để tính căn bậc hai
Cho bảng dữ liệu sau:
| Ô | Giá trị | Hàm SQRT |
|---|---|---|
| A1 | 9 | =SQRT(A1) |
| A2 | 144 | =SQRT(A2) |
| A3 | 625 | =SQRT(A3) |
Kết quả:
| Ô | Giá trị | Hàm SQRT | Kết quả |
|---|---|---|---|
| A1 | 9 | =SQRT(A1) | 3 |
| A2 | 144 | =SQRT(A2) | 12 |
| A3 | 625 | =SQRT(A3) | 25 |
Ví dụ 3: Xử lý số âm bằng hàm ABS
Như đã đề cập, hàm SQRT không hoạt động với số âm. Để khắc phục điều này, bạn có thể sử dụng hàm ABS để chuyển số âm thành số dương trước khi tính căn bậc hai:
| Số | Hàm SQRT | Kết quả |
|---|---|---|
| -16 | =SQRT(ABS(-16)) | 4 |
| -25 | =SQRT(ABS(-25)) | 5 |
Ví dụ 4: Làm tròn kết quả bằng hàm ROUND
Trong nhiều trường hợp, kết quả của hàm SQRT có thể là một số thập phân dài. Để làm tròn kết quả đến một số chữ số thập phân nhất định, bạn có thể sử dụng hàm ROUND:
| Số | Hàm SQRT | Hàm ROUND | Kết quả |
|---|---|---|---|
| 10 | =SQRT(10) | =ROUND(SQRT(10), 2) | 3.16 |
| 20 | =SQRT(20) | =ROUND(SQRT(20), 1) | 4.5 |
Trong đó:
- Number: Là số bạn muốn làm tròn.
- Num_digits: Là số chữ số thập phân bạn muốn giữ lại.
5. Mẹo Sử Dụng Hàm SQRT Hiệu Quả
Để sử dụng hàm SQRT một cách hiệu quả nhất, hãy ghi nhớ những mẹo sau:
- Luôn kiểm tra giá trị đầu vào: Đảm bảo rằng số bạn muốn tính căn bậc hai là một số dương. Nếu không, hãy sử dụng hàm ABS để chuyển số âm thành số dương trước.
- Kết hợp với các hàm khác: Hàm SQRT có thể được kết hợp với nhiều hàm khác trong Excel để thực hiện các phép tính phức tạp hơn. Ví dụ, bạn có thể kết hợp hàm SQRT với hàm IF để tạo ra một công thức có điều kiện.
- Sử dụng định dạng số phù hợp: Để hiển thị kết quả của hàm SQRT một cách chính xác, hãy sử dụng định dạng số phù hợp. Bạn có thể chọn số chữ số thập phân hiển thị, hoặc sử dụng các định dạng đặc biệt như phân số hoặc phần trăm.
- Tham khảo tài liệu справка của Excel: Nếu bạn gặp bất kỳ khó khăn nào trong quá trình sử dụng hàm SQRT, đừng ngần ngại tham khảo tài liệu hướng dẫn chi tiết của Excel.
6. So Sánh Hàm SQRT Với Các Hàm Tương Tự
Ngoài hàm SQRT, Excel còn cung cấp một số hàm khác có chức năng tương tự, hoặc có thể được sử dụng để thực hiện các phép tính liên quan đến căn bậc hai:
| Hàm | Chức năng | Ví dụ |
|---|---|---|
| SQRT | Tính căn bậc hai của một số dương. | =SQRT(25) trả về 5. |
| POWER | Tính lũy thừa của một số. Có thể được sử dụng để tính căn bậc hai bằng cách sử dụng số mũ 0.5. | =POWER(25, 0.5) trả về 5. |
| SQRTPI | Tính căn bậc hai của một số nhân với số Pi (π). | =SQRTPI(2) trả về căn bậc hai của (2 * π). |
| IMABS | Tính trị tuyệt đối (module) của một số phức. | =IMABS("3+4i") trả về 5 (trị tuyệt đối của số phức 3+4i là √(3²+4²) = 5). |
| COMPLEX | Tạo một số phức từ phần thực và phần ảo. | =COMPLEX(3, 4, "i") tạo số phức 3+4i. |
| IMSQRT | Tính căn bậc hai của một số phức. | =IMSQRT("3+4i") trả về căn bậc hai của số phức 3+4i. |
| EXP | Trả về số e (cơ số của logarit tự nhiên, xấp xỉ 2.71828) được nâng lên lũy thừa của một số đã cho. | =EXP(1) trả về giá trị của e (khoảng 2.71828). |
| LN | Trả về logarit tự nhiên của một số. Logarit tự nhiên dựa trên hằng số e (xấp xỉ 2.71828). | =LN(2.71828) trả về 1. |
| LOG | Trả về logarit của một số theo cơ số đã chỉ định. | =LOG(100, 10) trả về 2 (logarit cơ số 10 của 100 là 2). |
| LOG10 | Trả về logarit cơ số 10 của một số. | =LOG10(100) trả về 2. |
| FACT | Trả về giai thừa của một số. Giai thừa của một số bằng tích của tất cả các số nguyên dương nhỏ hơn hoặc bằng số đó. | =FACT(5) trả về 120 (5! = 5 4 3 2 1 = 120). |
| COMBIN | Trả về số lượng tổ hợp có thể có từ một số mục nhất định. COMBIN được sử dụng để xác định tổng số nhóm có thể có cho một số mục đã cho. | =COMBIN(5, 2) trả về 10 (số lượng tổ hợp 2 mục từ 5 mục). |
| PERMUT | Trả về số lượng hoán vị cho một số mục nhất định. PERMUT được sử dụng để xác định số lượng nhóm có thể có trong đó thứ tự nội bộ có ý nghĩa. | =PERMUT(5, 2) trả về 20 (số lượng hoán vị 2 mục từ 5 mục). |
| RADIANS | Chuyển đổi độ thành radian. | =RADIANS(180) trả về 3.141592654 (π radian tương đương với 180 độ). |
| DEGREES | Chuyển đổi radian thành độ. | =DEGREES(3.141592654) trả về 180. |
| SIN, COS, TAN | Trả về sin, cosin và tang của một góc đã cho (tính bằng radian). | =SIN(RADIANS(30)) trả về 0.5 (sin của 30 độ). |
| ASIN, ACOS, ATAN | Trả về arcsin, arccos và arctan của một số. | =ASIN(0.5) trả về 0.523598776 (arcsin của 0.5). |
| ATAN2 | Trả về arctan của tọa độ x và y. | =ATAN2(1, 1) trả về 0.785398163 (arctan của 1/1). |
| ROUND | Làm tròn một số đến số chữ số đã chỉ định. | =ROUND(3.14159, 2) trả về 3.14. |
| ROUNDUP | Làm tròn một số lên đến số chữ số đã chỉ định. | =ROUNDUP(3.14159, 2) trả về 3.15. |
| ROUNDDOWN | Làm tròn một số xuống đến số chữ số đã chỉ định. | =ROUNDDOWN(3.14159, 2) trả về 3.14. |
| INT | Làm tròn một số xuống số nguyên gần nhất. | =INT(3.9) trả về 3. |
| TRUNC | Cắt bớt một số thành một số nguyên bằng cách loại bỏ phần thập phân của số đó. | =TRUNC(3.9) trả về 3. |
| MOD | Trả về phần dư sau khi một số được chia cho một số khác. | =MOD(10, 3) trả về 1 (10 chia 3 dư 1). |
| RAND | Trả về một số ngẫu nhiên lớn hơn hoặc bằng 0 và nhỏ hơn 1. | =RAND() trả về một số ngẫu nhiên giữa 0 và 1. |
| RANDBETWEEN | Trả về một số nguyên ngẫu nhiên giữa các số bạn chỉ định. | =RANDBETWEEN(1, 100) trả về một số nguyên ngẫu nhiên giữa 1 và 100. |
| ROMAN | Chuyển đổi một số Ả Rập thành số La Mã, dưới dạng văn bản. | =ROMAN(4) trả về IV. |
| ARABIC | Chuyển đổi số La Mã thành số Ả Rập. | =ARABIC("IV") trả về 4. |
| GCD | Trả về ước số chung lớn nhất. | =GCD(24, 36) trả về 12. |
| LCM | Trả về bội số chung nhỏ nhất. | =LCM(12, 18) trả về 36. |
7. Hàm SQRTPI Là Gì?
Hàm SQRTPI là một biến thể của hàm SQRT, được sử dụng để tính căn bậc hai của một số nhân với số Pi (π ≈ 3.14159).
Công thức:
=SQRTPI(number)
Trong đó:
- Number: Là số mà bạn muốn tính căn bậc hai sau khi nhân với Pi.
Ví dụ:
=SQRTPI(2) sẽ trả về kết quả là √(2 * π) ≈ 2.5066.
Lưu ý:
- Tương tự như hàm SQRT, hàm SQRTPI cũng chỉ hoạt động với các số dương.
8. Ứng Dụng Của Hàm SQRTPI Trong Ẩm Thực
Mặc dù không phổ biến bằng hàm SQRT, hàm SQRTPI vẫn có thể được ứng dụng trong một số trường hợp cụ thể trong lĩnh vực ẩm thực:
-
Tính toán diện tích hình tròn khi biết chu vi: Nếu bạn biết chu vi của một chiếc bánh tròn và muốn tính diện tích của nó, bạn có thể sử dụng công thức:
- Diện tích = (Chu vi)² / (4 * π)
- Để đơn giản hóa phép tính, bạn có thể sử dụng hàm SQRTPI: Diện tích = (Chu vi / 2)² / π = (Chu vi / (2 * √(π)))²
- Trong Excel, bạn có thể nhập công thức:
=(Chu vi / (2 * SQRTPI(1)))^2
-
Tính toán các thông số liên quan đến hình cầu: Trong một số công thức nấu ăn hoặc trang trí bánh, bạn có thể cần tính toán các thông số liên quan đến hình cầu, chẳng hạn như thể tích hoặc diện tích bề mặt. Các công thức này thường liên quan đến số Pi và có thể được đơn giản hóa bằng cách sử dụng hàm SQRTPI.
9. Các Lỗi Thường Gặp Khi Sử Dụng Hàm SQRT Và Cách Khắc Phục
Trong quá trình sử dụng hàm SQRT, bạn có thể gặp phải một số lỗi sau:
- Lỗi #NUM!: Lỗi này xảy ra khi bạn nhập một số âm vào hàm SQRT. Để khắc phục, hãy đảm bảo rằng số bạn nhập là một số dương, hoặc sử dụng hàm ABS để chuyển số âm thành số dương trước khi tính căn bậc hai.
- Lỗi #VALUE!: Lỗi này xảy ra khi bạn nhập một giá trị không phải là số vào hàm SQRT. Hãy kiểm tra lại giá trị bạn nhập và đảm bảo rằng nó là một số hợp lệ.
- Kết quả không chính xác: Đôi khi, kết quả của hàm SQRT có thể không chính xác do sai số làm tròn. Để khắc phục, hãy sử dụng hàm ROUND để làm tròn kết quả đến một số chữ số thập phân nhất định.
10. Kết Hợp Hàm SQRT Với Các Hàm Khác Để Giải Quyết Bài Toán Thực Tế
Để tăng tính ứng dụng của hàm SQRT, bạn có thể kết hợp nó với các hàm khác trong Excel để giải quyết các bài toán thực tế phức tạp hơn. Dưới đây là một vài ví dụ:
-
Tính độ dài đường chéo của hình chữ nhật: Cho biết chiều dài và chiều rộng của một hình chữ nhật, bạn có thể tính độ dài đường chéo bằng định lý Pythagoras:
- Đường chéo = √(Chiều dài² + Chiều rộng²)
- Trong Excel, bạn có thể nhập công thức:
=SQRT(Chiều dài^2 + Chiều rộng^2)
-
Tính khoảng cách giữa hai điểm trên mặt phẳng: Cho biết tọa độ của hai điểm (x1, y1) và (x2, y2), bạn có thể tính khoảng cách giữa chúng bằng công thức:
- Khoảng cách = √((x2 – x1)² + (y2 – y1)²)
- Trong Excel, bạn có thể nhập công thức:
=SQRT((x2 - x1)^2 + (y2 - y1)^2)
-
Tính thời gian rơi tự do của một vật: Cho biết độ cao của một vật, bạn có thể tính thời gian rơi tự do của vật đó bằng công thức:
- Thời gian = √(2 * Độ cao / Gia tốc trọng trường)
- Trong Excel, bạn có thể nhập công thức:
=SQRT(2 * Độ cao / 9.81)(với gia tốc trọng trường ≈ 9.81 m/s²)
11. Tìm Hiểu Thêm Về Các Hàm Toán Học Khác Trong Excel
Ngoài hàm SQRT, Excel còn cung cấp rất nhiều hàm toán học hữu ích khác, giúp bạn thực hiện các phép tính từ cơ bản đến nâng cao. Hãy dành thời gian tìm hiểu và làm quen với các hàm này để nâng cao kỹ năng sử dụng Excel của bạn. Bạn có thể tham khảo danh sách các hàm toán học phổ biến trong Excel và tìm hiểu về chức năng, cú pháp và cách sử dụng của chúng.
12. Cập Nhật Xu Hướng Ẩm Thực Tại Mỹ
Để làm phong phú thêm kiến thức ẩm thực của bạn, hãy cùng balocco.net điểm qua một số xu hướng ẩm thực đang thịnh hành tại Mỹ:
| Xu hướng | Mô tả | Ví dụ |
|---|---|---|
| Ẩm thực bền vững | Ưu tiên sử dụng các nguyên liệu có nguồn gốc địa phương, theo mùa và thân thiện với môi trường. | Nhà hàng sử dụng rau củ quả từ trang trại địa phương, giảm thiểu rác thải thực phẩm. |
| Ẩm thực thực vật | Các món ăn thuần chay hoặc có nguồn gốc từ thực vật ngày càng trở nên phổ biến, đáp ứng nhu cầu của những người ăn chay và quan tâm đến sức khỏe. | Các món burger chay, pizza chay, các loại sữa thực vật (sữa hạnh nhân, sữa đậu nành). |
| Ẩm thực quốc tế | Sự kết hợp giữa các hương vị và kỹ thuật nấu ăn từ các quốc gia khác nhau tạo ra những món ăn độc đáo và hấp dẫn. | Món sushi kiểu Mexico, món mì Ý kết hợp với gia vị châu Á. |
| Ẩm thực lành mạnh | Tập trung vào các món ăn giàu dinh dưỡng, ít calo, đường và chất béo. | Các món salad trộn, sinh tố trái cây, các món ăn chế biến từ ngũ cốc nguyên hạt. |
| Ẩm thực trải nghiệm | Các nhà hàng và quán ăn không chỉ chú trọng đến chất lượng món ăn mà còn tạo ra những trải nghiệm độc đáo và đáng nhớ cho khách hàng. | Các buổi trình diễn nấu ăn trực tiếp, các lớp học nấu ăn, các tour du lịch ẩm thực. |
| Sử dụng công nghệ trong ẩm thực | Ứng dụng các công nghệ mới để nâng cao trải nghiệm ẩm thực và tối ưu hóa quy trình sản xuất và phục vụ. | Sử dụng máy in 3D để tạo ra các món ăn độc đáo, ứng dụng đặt đồ ăn trực tuyến, robot phục vụ bàn. |
13. FAQ – Các Câu Hỏi Thường Gặp Về Hàm SQRT
-
Hàm SQRT dùng để làm gì?
Hàm SQRT dùng để tính căn bậc hai của một số dương.
-
Cú pháp của hàm SQRT là gì?
Cú pháp của hàm SQRT là
=SQRT(number), trong đó number là số bạn muốn tính căn bậc hai. -
Hàm SQRT có thể tính căn bậc hai của số âm không?
Không, hàm SQRT chỉ hoạt động với các số dương. Nếu bạn nhập một số âm, Excel sẽ trả về lỗi #NUM!.
-
Làm thế nào để tính căn bậc hai của số âm trong Excel?
Bạn có thể sử dụng hàm ABS để chuyển số âm thành số dương trước khi tính căn bậc hai:
=SQRT(ABS(number)). -
Hàm SQRTPI dùng để làm gì?
Hàm SQRTPI dùng để tính căn bậc hai của một số nhân với số Pi (π).
-
Làm thế nào để làm tròn kết quả của hàm SQRT?
Bạn có thể sử dụng hàm ROUND để làm tròn kết quả của hàm SQRT:
=ROUND(SQRT(number), num_digits), trong đó num_digits là số chữ số thập phân bạn muốn giữ lại. -
Có hàm nào khác trong Excel có thể thay thế hàm SQRT không?
Có, bạn có thể sử dụng hàm POWER với số mũ 0.5 để tính căn bậc hai:
=POWER(number, 0.5). -
Tại sao kết quả của hàm SQRT lại không chính xác?
Kết quả của hàm SQRT có thể không chính xác do sai số làm tròn. Để khắc phục, hãy sử dụng hàm ROUND để làm tròn kết quả đến một số chữ số thập phân nhất định.
-
Hàm SQRT có thể được sử dụng trong lĩnh vực ẩm thực không?
Có, hàm SQRT có thể được sử dụng để tính toán diện tích, thể tích, tỉ lệ thành phần, hoặc trong các công thức phức tạp hơn liên quan đến nhiệt độ và thời gian nấu nướng.
-
Tôi có thể tìm hiểu thêm về các hàm toán học khác trong Excel ở đâu?
Bạn có thể tham khảo tài liệu справка của Excel hoặc tìm kiếm trên internet để tìm hiểu thêm về các hàm toán học khác trong Excel.
14. Lời Kêu Gọi Hành Động
Bạn đã sẵn sàng khám phá thế giới ẩm thực đầy thú vị và tiện lợi với hàm SQRT trong Excel chưa? Hãy truy cập balocco.net ngay hôm nay để khám phá bộ sưu tập công thức nấu ăn phong phú, mẹo vặt hữu ích và kết nối với cộng đồng những người đam mê ẩm thực tại Mỹ.
Tại balocco.net, bạn sẽ tìm thấy:
- Hàng ngàn công thức nấu ăn được phân loại theo món ăn, nguyên liệu, quốc gia và chế độ ăn uống.
- Các bài viết hướng dẫn chi tiết về các kỹ thuật nấu ăn cơ bản và nâng cao.
- Gợi ý về nhà hàng, quán ăn và các địa điểm ẩm thực nổi tiếng.
- Các công cụ và tài nguyên để lên kế hoạch bữa ăn và quản lý thực phẩm.
- Một cộng đồng trực tuyến cho những người yêu thích ẩm thực giao lưu và chia sẻ kinh nghiệm.
Đừng bỏ lỡ cơ hội trở thành một đầu bếp tài ba và khám phá những trải nghiệm ẩm thực tuyệt vời cùng balocco.net!
Thông tin liên hệ:
- Address: 175 W Jackson Blvd, Chicago, IL 60604, United States
- Phone: +1 (312) 563-8200
- Website: balocco.net