Cos Là Gì? Công Thức Cosin, Ứng Dụng & Ví Dụ Chi Tiết

Bạn đang tìm kiếm định nghĩa chính xác về cos, công thức cosin và cách áp dụng nó trong các bài toán thực tế? Hãy cùng balocco.net khám phá tất tần tật về cos và những ứng dụng thú vị của nó trong hình học và cuộc sống, được trình bày một cách dễ hiểu nhất!

1. Cos Là Gì? Giải Mã Bí Ẩn Của Hàm Cosin

Cos, hay còn gọi là cosin, là một trong những hàm số lượng giác cơ bản, đóng vai trò quan trọng trong hình học và nhiều lĩnh vực khác. Vậy Cos Là Gì và tại sao nó lại quan trọng đến vậy?

Cosin của một góc trong tam giác vuông được định nghĩa là tỷ số giữa cạnh kề của góc đó và cạnh huyền. Nói một cách dễ hiểu hơn, nếu bạn có một tam giác vuông, hãy chọn một góc (không phải góc vuông). Cạnh kề là cạnh nằm giữa góc bạn chọn và góc vuông, còn cạnh huyền là cạnh dài nhất của tam giác. Tỷ lệ giữa hai cạnh này chính là cosin của góc đó. Công thức cosin, ký hiệu là cos(x), là một công cụ mạnh mẽ giúp bạn tính toán các yếu tố liên quan đến tam giác, từ đó giải quyết nhiều bài toán thực tế.

1.1. Cos trong Toán Học Lượng Giác

Trong toán học lượng giác, cosin là một hàm số tuần hoàn với chu kỳ 2π (360 độ). Điều này có nghĩa là giá trị của cosin lặp lại sau mỗi khoảng 2π. Hàm cosin có nhiều tính chất quan trọng, chẳng hạn như:

• Giá trị: Giá trị của cosin luôn nằm trong khoảng từ -1 đến 1.
• Tính chẵn: Cosin là một hàm số chẵn, nghĩa là cos(-x) = cos(x).
• Đạo hàm: Đạo hàm của cos(x) là -sin(x), trong đó sin(x) là hàm sin.

Các tính chất này giúp chúng ta hiểu rõ hơn về cosin và sử dụng nó một cách hiệu quả trong các bài toán lượng giác.

1.2. Cos trong Hình Học Phẳng

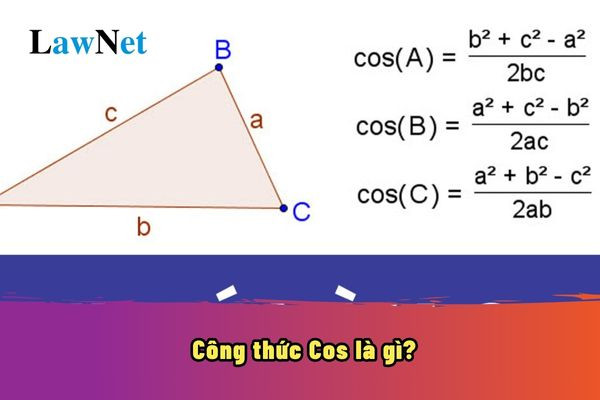Công thức cosin, cách tính cosin và giá trị cosin của các góc đặc biệt

Cosin không chỉ là một khái niệm trừu tượng trong sách giáo khoa, mà còn có nhiều ứng dụng thực tế trong hình học phẳng. Một trong những ứng dụng quan trọng nhất của cosin là định lý cosin. Định lý này cho phép bạn tính độ dài cạnh của một tam giác bất kỳ khi biết độ dài hai cạnh còn lại và góc xen giữa chúng.

Công thức định lý cosin như sau:

c² = a² + b² - 2ab * cos(C)

Trong đó:

• c là độ dài cạnh đối diện với góc C.
• a, b là độ dài hai cạnh còn lại.
• C là góc xen giữa hai cạnh a và b.

Định lý cosin là một công cụ hữu ích để giải các bài toán liên quan đến tam giác, chẳng hạn như tính khoảng cách giữa hai điểm trên bản đồ hoặc xác định góc giữa hai đường thẳng.

1.3. Cos trong Ứng Dụng Thực Tế

Không chỉ giới hạn trong sách vở, cos còn hiện diện trong nhiều lĩnh vực của đời sống. Từ xây dựng, thiết kế đến định vị GPS, cos đều đóng vai trò quan trọng.

• Xây dựng và thiết kế: Các kiến trúc sư và kỹ sư sử dụng cosin để tính toán góc và khoảng cách trong các công trình xây dựng, đảm bảo tính chính xác và an toàn.
• Định vị GPS: Hệ thống GPS sử dụng cosin để xác định vị trí của bạn trên Trái Đất dựa trên tín hiệu từ các vệ tinh.
• Vật lý: Cosin được sử dụng để phân tích các lực và chuyển động trong vật lý, giúp chúng ta hiểu rõ hơn về thế giới xung quanh.
• Âm nhạc: Cosin được sử dụng để tạo ra các âm thanh và hiệu ứng âm nhạc, mang đến cho chúng ta những trải nghiệm âm nhạc tuyệt vời.

Như vậy, cos không chỉ là một khái niệm toán học khô khan, mà còn là một công cụ mạnh mẽ giúp chúng ta giải quyết nhiều vấn đề trong cuộc sống.

2. Khám Phá Công Thức Cosin: “Chìa Khóa” Giải Quyết Bài Toán Tam Giác

Công thức cosin, như đã đề cập ở trên, là một công cụ vô cùng hữu ích trong việc giải các bài toán liên quan đến tam giác. Nhưng làm thế nào để sử dụng công thức này một cách hiệu quả? Hãy cùng balocco.net khám phá chi tiết về công thức cosin và cách áp dụng nó vào các bài toán cụ thể.

2.1. Ba Dạng Công Thức Cosin

Định lý cosin có thể được biểu diễn dưới ba dạng khác nhau, tùy thuộc vào yếu tố bạn muốn tính toán:

1. Tính cạnh c:

   c² = a² + b² - 2ab * cos(C)

   Công thức này được sử dụng khi bạn biết độ dài hai cạnh a, b và góc C xen giữa chúng, và muốn tính độ dài cạnh c đối diện với góc C.

2. Tính cạnh b:

   b² = a² + c² - 2ac * cos(B)

   Tương tự, công thức này được sử dụng khi bạn biết độ dài hai cạnh a, c và góc B xen giữa chúng, và muốn tính độ dài cạnh b đối diện với góc B.

3. Tính góc C:

   cos(C) = (a² + b² - c²) / (2ab)

   Công thức này được sử dụng khi bạn biết độ dài ba cạnh a, b, c của tam giác, và muốn tính góc C đối diện với cạnh c.

Việc nắm vững ba dạng công thức này giúp bạn linh hoạt hơn trong việc giải các bài toán khác nhau.

2.2. Điều Kiện Áp Dụng Công Thức Cosin

Không phải lúc nào bạn cũng có thể sử dụng công thức cosin. Để áp dụng công thức này một cách chính xác, bạn cần đảm bảo rằng các điều kiện sau được đáp ứng:

• Tam giác: Công thức cosin chỉ áp dụng cho tam giác, không áp dụng cho các hình khác.
• Thông tin: Bạn cần biết ít nhất ba yếu tố của tam giác, bao gồm độ dài hai cạnh và góc xen giữa chúng (để tính cạnh còn lại), hoặc độ dài ba cạnh (để tính góc).
• Đơn vị đo: Đảm bảo rằng các cạnh và góc được đo bằng cùng một đơn vị (ví dụ: cm, độ).

Nếu các điều kiện này không được đáp ứng, bạn cần sử dụng các phương pháp khác để giải bài toán.

2.3. Ví Dụ Minh Họa

Để hiểu rõ hơn về cách sử dụng công thức cosin, hãy cùng xem xét một vài ví dụ cụ thể:

Ví dụ 1: Cho tam giác ABC có AB = 5cm, AC = 7cm và góc BAC = 60 độ. Tính độ dài cạnh BC.

Giải:

Áp dụng công thức cosin, ta có:

BC² = AB² + AC² - 2 * AB * AC * cos(BAC)
BC² = 5² + 7² - 2 * 5 * 7 * cos(60°)
BC² = 25 + 49 - 35
BC² = 39
BC ≈ 6.24 cm

Vậy độ dài cạnh BC xấp xỉ 6.24 cm.

Ví dụ 2: Cho tam giác ABC có AB = 6cm, BC = 8cm và AC = 10cm. Tính góc BAC.

Giải:

Áp dụng công thức cosin, ta có:

cos(BAC) = (AB² + AC² - BC²) / (2 * AB * AC)
cos(BAC) = (6² + 10² - 8²) / (2 * 6 * 10)
cos(BAC) = 72 / 120
cos(BAC) = 0.6
BAC ≈ 53.13°

Vậy góc BAC xấp xỉ 53.13 độ.

2.4. Mẹo Sử Dụng Công Thức Cosin Hiệu Quả

Để sử dụng công thức cosin một cách hiệu quả nhất, hãy ghi nhớ những mẹo sau:

• Xác định yếu tố cần tìm: Trước khi bắt đầu tính toán, hãy xác định rõ yếu tố bạn muốn tìm (cạnh hay góc).
• Chọn công thức phù hợp: Chọn công thức cosin phù hợp với yếu tố bạn muốn tìm và thông tin đã biết.
• Kiểm tra điều kiện: Đảm bảo rằng các điều kiện áp dụng công thức cosin được đáp ứng.
• Tính toán cẩn thận: Thực hiện các phép tính một cách cẩn thận để tránh sai sót.
• Kiểm tra kết quả: Sau khi tính toán xong, hãy kiểm tra lại kết quả để đảm bảo tính chính xác.

Với những mẹo này, bạn sẽ có thể sử dụng công thức cosin một cách thành thạo và giải quyết các bài toán tam giác một cách dễ dàng.

3. Học Sinh Học Cosin Ở Lớp Mấy?

Vậy, khi nào học sinh bắt đầu làm quen với cosin và công thức cosin trong chương trình học?

Theo chương trình giáo dục phổ thông môn Toán hiện hành tại Việt Nam, học sinh sẽ được giới thiệu về các hàm số lượng giác, bao gồm cosin, sin, tang và cotang, từ lớp 9.

3.1. Nội Dung Chương Trình Lớp 9

Trong chương trình Toán lớp 9, học sinh sẽ được học về:

• Tỉ số lượng giác của góc nhọn: Định nghĩa và tính chất của các tỉ số lượng giác sin, cos, tan, cot của một góc nhọn trong tam giác vuông.
• Một số hệ thức về cạnh và góc trong tam giác vuông: Các công thức liên hệ giữa các cạnh và góc trong tam giác vuông, giúp giải các bài toán liên quan.
• Ứng dụng thực tế: Giải các bài toán thực tế liên quan đến tỉ số lượng giác của góc nhọn, ví dụ như tính chiều cao của một tòa nhà hoặc khoảng cách giữa hai điểm.

Tuy nhiên, công thức cosin tổng quát cho tam giác bất kỳ thường được giới thiệu ở các lớp cao hơn, như lớp 10 hoặc 11, khi học sinh đã có kiến thức vững chắc về lượng giác và hình học.

3.2. Mục Tiêu Đánh Giá Kết Quả Giáo Dục Môn Toán Lớp 9

Việc đánh giá kết quả giáo dục môn Toán lớp 9 nhằm cung cấp thông tin chính xác, kịp thời và có giá trị về sự phát triển năng lực và sự tiến bộ của học sinh. Đồng thời, việc đánh giá này cũng giúp điều chỉnh các hoạt động dạy học, đảm bảo sự tiến bộ của từng học sinh và nâng cao chất lượng giáo dục môn Toán nói riêng và chất lượng giáo dục nói chung.

3.2.1. Hình Thức và Phương Pháp Đánh Giá

Việc đánh giá kết hợp nhiều hình thức (đánh giá quá trình, đánh giá thường xuyên, đánh giá định kỳ) và nhiều phương pháp (quan sát, ghi lại quá trình thực hiện, vấn đáp, trắc nghiệm khách quan, tự luận, kiểm tra viết, bài tập thực hành, các dự án/sản phẩm học tập, thực hiện nhiệm vụ thực tiễn,…) vào những thời điểm thích hợp.

• Đánh giá quá trình: Do giáo viên phụ trách môn học tổ chức, kết hợp với đánh giá của giáo viên các môn học khác, của bản thân học sinh được đánh giá và của các học sinh khác trong tổ, trong lớp hoặc đánh giá của cha mẹ học sinh.
• Đánh giá định kỳ: Nhằm đánh giá việc thực hiện các mục tiêu học tập. Kết quả đánh giá định kỳ và đánh giá tổng kết được sử dụng để chứng nhận cấp độ học tập, công nhận thành tích của học sinh.

3.2.2. Đánh Giá Năng Lực Học Sinh

Việc đánh giá năng lực học sinh được thực hiện thông qua các bằng chứng biểu hiện kết quả đạt được trong quá trình thực hiện các hành động của học sinh. Tiến trình đánh giá gồm các bước cơ bản như: xác định mục đích đánh giá; xác định bằng chứng cần thiết; lựa chọn các phương pháp, công cụ đánh giá thích hợp; thu thập bằng chứng; giải thích bằng chứng và đưa ra nhận xét.

Giáo viên cần chú trọng việc lựa chọn phương pháp, công cụ đánh giá các thành tố của năng lực toán học. Cụ thể:

• Đánh giá năng lực tư duy và lập luận toán học: Sử dụng các câu hỏi (nói, viết), bài tập,… đòi hỏi học sinh phải trình bày, so sánh, phân tích, tổng hợp, hệ thống hóa kiến thức; vận dụng kiến thức toán học để giải thích, lập luận.
• Đánh giá năng lực mô hình hóa toán học: Lựa chọn những tình huống trong thực tiễn làm xuất hiện bài toán toán học. Từ đó, đòi hỏi học sinh phải xác định được mô hình toán học (gồm công thức, phương trình, bảng biểu, đồ thị,…) cho tình huống xuất hiện trong bài toán thực tiễn; giải quyết được những vấn đề toán học trong mô hình được thiết lập; thể hiện và đánh giá được lời giải trong ngữ cảnh thực tiễn và cải tiến được mô hình nếu cách giải quyết không phù hợp.
• Đánh giá năng lực giải quyết vấn đề toán học: Sử dụng các phương pháp như yêu cầu người học nhận dạng tình huống, phát hiện và trình bày vấn đề cần giải quyết; mô tả, giải thích các thông tin ban đầu, mục tiêu, mong muốn của tình huống vấn đề đang xem xét.
• Đánh giá năng lực giao tiếp toán học: Yêu cầu người học nghe hiểu, đọc hiểu, ghi chép (tóm tắt), phân tích, lựa chọn, trích xuất được các thông tin toán học cơ bản, trọng tâm trong văn bản nói hoặc viết; sử dụng được ngôn ngữ toán học kết hợp với ngôn ngữ thông thường trong việc trình bày, diễn đạt, nêu câu hỏi, thảo luận, tranh luận các nội dung, ý tưởng, giải pháp toán học trong sự tương tác với người khác.
• Đánh giá năng lực sử dụng công cụ, phương tiện học toán: Yêu cầu người học nhận biết được tên gọi, tác dụng, quy cách sử dụng, cách thức bảo quản, ưu điểm, hạn chế của các công cụ, phương tiện học toán; trình bày được cách sử dụng (hợp lý) công cụ, phương tiện học toán để thực hiện nhiệm vụ học tập hoặc để diễn tả những lập luận, chứng minh toán học.

Khi giáo viên lên kế hoạch bài học, cần thiết lập các tiêu chí và cách thức đánh giá để bảo đảm ở cuối mỗi bài học học sinh đạt được các yêu cầu cơ bản dựa trên các tiêu chí đã nêu, trước khi thực hiện các hoạt động học tập tiếp theo.

4. Bài Tập Vận Dụng Công Thức Cosin

Để củng cố kiến thức và rèn luyện kỹ năng sử dụng công thức cosin, hãy cùng balocco.net thử sức với một số bài tập vận dụng sau:

Bài 1: Một chiếc thuyền đi từ điểm A đến điểm B với khoảng cách 10 km. Sau đó, thuyền rẽ hướng 60 độ và đi tiếp đến điểm C với khoảng cách 8 km. Tính khoảng cách từ điểm A đến điểm C.

Bài 2: Một người đứng ở điểm A và nhìn thấy đỉnh của một tòa nhà cao tầng với góc nâng 30 độ. Sau đó, người đó đi thẳng về phía tòa nhà thêm 50 mét và nhìn thấy đỉnh của tòa nhà với góc nâng 45 độ. Tính chiều cao của tòa nhà.

Bài 3: Cho tam giác ABC có AB = 4cm, BC = 6cm và AC = 5cm. Tính diện tích của tam giác ABC.

Hướng dẫn giải:

• Bài 1: Sử dụng công thức cosin để tính cạnh AC.
• Bài 2: Sử dụng tỉ số lượng giác và công thức cosin để giải bài toán.
• Bài 3: Sử dụng công thức Heron để tính diện tích tam giác khi biết độ dài ba cạnh.

5. Câu Hỏi Thường Gặp Về Cos

Để giúp bạn hiểu rõ hơn về cos và công thức cosin, balocco.net đã tổng hợp một số câu hỏi thường gặp và câu trả lời chi tiết:

1. Cos là gì? Cos là tỷ số giữa cạnh kề và cạnh huyền của một góc trong tam giác vuông.
2. Công thức cosin là gì? Công thức cosin là một công thức quan trọng trong hình học, cho phép tính độ dài cạnh hoặc góc của một tam giác bất kỳ.
3. Khi nào nên sử dụng công thức cosin? Bạn nên sử dụng công thức cosin khi biết độ dài hai cạnh và góc xen giữa chúng (để tính cạnh còn lại), hoặc khi biết độ dài ba cạnh (để tính góc).
4. Cos có giá trị lớn nhất và nhỏ nhất là bao nhiêu? Giá trị lớn nhất của cos là 1 và giá trị nhỏ nhất là -1.
5. Cos của góc 0 độ bằng bao nhiêu? Cos của góc 0 độ bằng 1.
6. Cos của góc 90 độ bằng bao nhiêu? Cos của góc 90 độ bằng 0.
7. Cos của góc 180 độ bằng bao nhiêu? Cos của góc 180 độ bằng -1.
8. Công thức cosin có thể áp dụng cho tam giác vuông không? Có, công thức cosin có thể áp dụng cho tam giác vuông, nhưng trong trường hợp này, nó sẽ trở thành định lý Pytago.
9. Làm thế nào để nhớ công thức cosin? Bạn có thể nhớ công thức cosin bằng cách liên tưởng đến định lý Pytago và thêm một thành phần điều chỉnh liên quan đến góc.
10. Cos có ứng dụng gì trong thực tế? Cos có nhiều ứng dụng trong thực tế, chẳng hạn như xây dựng, thiết kế, định vị GPS, vật lý và âm nhạc.

6. Lời Kết

Hy vọng bài viết này đã giúp bạn hiểu rõ hơn về cos, công thức cosin và những ứng dụng thú vị của nó. Nếu bạn muốn khám phá thêm nhiều công thức nấu ăn ngon, mẹo vặt hữu ích và thông tin ẩm thực đa dạng, hãy truy cập ngay balocco.net!

Bạn đang tìm kiếm công thức nấu ăn mới, muốn học hỏi các kỹ năng nấu nướng đỉnh cao, hay đơn giản chỉ muốn kết nối với cộng đồng những người đam mê ẩm thực tại Mỹ? Hãy đến với balocco.net ngay hôm nay!

Địa chỉ: 175 W Jackson Blvd, Chicago, IL 60604, United States

Điện thoại: +1 (312) 563-8200

Website: balocco.net